4. Identification des caractéristiques dynamiques de l'amortisseur

Objectifs : retrouver les mêmes résultats que précédemment et identifier les caractéristiques dynamiqude de l'amortisseur à l'aide de courbes.

Nous allons réaliser un calcul dynamique : c'est à dire que nous relions les effets (les mouvements) aux causes (les efforts).

Il faut donc tenir compte des masses (effet d'inertie). Nous tenons compte, seulement de la masse du chassis, pour cela ;

Modifier les caractéritique du chassis : "acquisition \ pièce \ modifier". Sélectionner la pièce en question et défnir sa masse à 200 kg.
Remarque : cette masse ne donnera pas lieu à la pesanteur.

L'action mécanique de la pesanteur est maintenant connue (la "ruse" précédente n'est plus nécéssaire). Elle a pour norme 2000 N.

Supprimer celle qui était inconnue, puis ajouter une action mécanique connue de 2000 N vers le bas.

Ajouter un effort d'amortissement (voir AN en 1° page) dans la liaison glissière modélisant l'amortisseur.

Nous allons maintenant procéder au calcul. Un calcul dynamique est plus difficile pour un ordinateur qu'un calcul statique. Il doit procéder à un calcul d'intégrale numérique : pour cela les points de calculs doivent être proche.

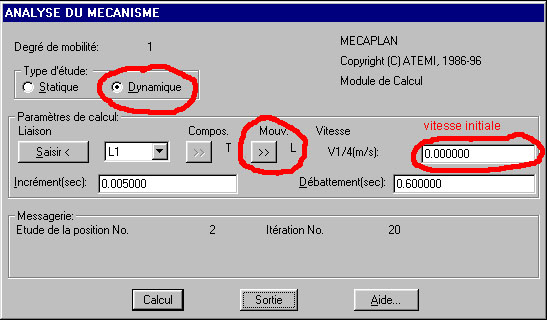
Lancer le calcul : demander une étude dynamique, un mouvement Libre (la vitesse dans le masse est alors la vitesse initiale). "Calcul".

Le logiciel va probablement signaler une position impossible à atteindre : l'incrément est trop grand, les points de calcul sont trop éloignés.

Rechercher la valeur maximale de l'incrément qui permette de résoudre le problème (entre deux tentatives de calcul avortées, il faut "abandonner" le calcul : c'est un bogue du logiciel).

Une fois que l'on a cette valeur maximale, rechercher un débattement le plus grand possible (pour bénéficier d'une étude la plus complète possible) sachant que 360 positions maxi. sont possibles.

Simuler les mouvements pour vérifier le bon fonctionnement du modèle.

Rechercher alors la position d'équilibre (utiliser des courbes). Comparer avec le résultat obtenu en étude statique.

Identification dynamique :

Tracer la courbe donnant la position du châssis en fonction du temps. Cette courbe ressemble à la réponse d'un système de quel ordre ? Peut-on comparer (justifier en discutant sur le "signal d'entrée").

A partir de cette courbe (que vous pouvez tracer, mais ce n'est pas nécessaire), identifier les caractéristiques de ce système : la pulsation propre n et le facteur d'amortissement z.
Rappels de cours si nécessaire.

Comparer avec les valeurs obtenues pour un système masse-ressort-amortisseur linéaire (cf formules ci-dessous) :

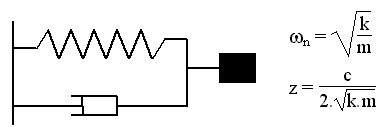
Conclure quant à la géométrie de la suspension.

Retour sommaire